Prima algoritms

Šajā apmācībā jūs uzzināsiet, kā darbojas Prim's algoritms. Jūs atradīsit arī Prim algoritma piemērus C, C ++, Java un Python.

Prim's algoritms ir minimālais aptveroša koka algoritms, kas ņem grafu kā ievadi un atrod šī grafika malu apakškopu, kas

veido koku, kas ietver katru virsotni
ir minimālā svaru summa starp visiem kokiem, kurus var veidot no diagrammas

Kā darbojas Prim algoritms

Tas ietilpst algoritmu klasē, ko sauc par mantkārīgiem algoritmiem, kuri atrod vietējo optimālu, cerot atrast globālo optimālu.

Mēs sākam no vienas virsotnes un turpinām pievienot malas ar mazāko svaru, līdz sasniedzam mērķi.

Prim algoritma ieviešanas darbības ir šādas:

Inicializējiet minimālo aptverošo koku ar nejauši izvēlētu virsotni.
Atrodiet visas malas, kas savieno koku ar jaunām virsotnēm, atrodiet minimālo un pievienojiet to kokam
Atkārtojiet 2. darbību, līdz iegūstam minimālo aptverošo koku

Prim's algoritma piemērs

Sākt ar svērto grafiku

Izvēlieties virsotne

izvēlēties īsāko malu no virsotnes un pievienot to

izvēlēties tuvāko virsotne vēl nav risinājuma

Izvēlieties tuvāko malas vēl nav risinājuma, ja ir vairākas izvēles, izvēlēties vienu izlases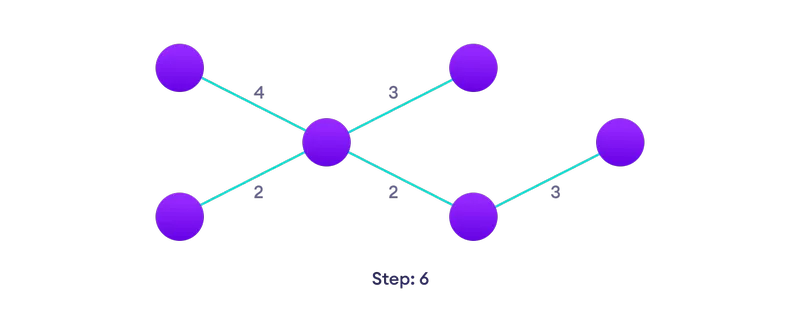

Atkārtojiet, līdz jums ir aptverošs koks

Prima algoritma pseidokods

Prim algoritma pseidokods parāda, kā mēs izveidojam divas virsotņu U un VU kopas. U satur apmeklēto virsotņu sarakstu, bet VU - to neapmeklēto virsotņu sarakstu. Pa vienam mēs pārvietojam virsotnes no kopas VU uz kopu U, savienojot vismazāko svara malu.

 T = ∅; U = ( 1 ); while (U ≠ V) let (u, v) be the lowest cost edge such that u ∈ U and v ∈ V - U; T = T ∪ ((u, v)) U = U ∪ (v)

Python, Java un C / C ++ piemēri

Lai gan tiek izmantots grafiku blakus esošās matricas attēlojums, šo algoritmu var arī ieviest, izmantojot Adjacency List, lai uzlabotu tā efektivitāti.

Python Java C C ++

 # Prim's Algorithm in Python INF = 9999999 # number of vertices in graph V = 5 # create a 2d array of size 5x5 # for adjacency matrix to represent graph G = ((0, 9, 75, 0, 0), (9, 0, 95, 19, 42), (75, 95, 0, 51, 66), (0, 19, 51, 0, 31), (0, 42, 66, 31, 0)) # create a array to track selected vertex # selected will become true otherwise false selected = (0, 0, 0, 0, 0) # set number of edge to 0 no_edge = 0 # the number of egde in minimum spanning tree will be # always less than(V - 1), where V is number of vertices in # graph # choose 0th vertex and make it true selected(0) = True # print for edge and weight print("Edge : Weight") while (no_edge  G(i)(j): minimum = G(i)(j) x = i y = j print(str(x) + "-" + str(y) + ":" + str(G(x)(y))) selected(y) = True no_edge += 1

 // Prim's Algorithm in Java import java.util.Arrays; class PGraph ( public void Prim(int G()(), int V) ( int INF = 9999999; int no_edge; // number of edge // create a array to track selected vertex // selected will become true otherwise false boolean() selected = new boolean(V); // set selected false initially Arrays.fill(selected, false); // set number of edge to 0 no_edge = 0; // the number of egde in minimum spanning tree will be // always less than (V -1), where V is number of vertices in // graph // choose 0th vertex and make it true selected(0) = true; // print for edge and weight System.out.println("Edge : Weight"); while (no_edge < V - 1) ( // For every vertex in the set S, find the all adjacent vertices // , calculate the distance from the vertex selected at step 1. // if the vertex is already in the set S, discard it otherwise // choose another vertex nearest to selected vertex at step 1. int min = INF; int x = 0; // row number int y = 0; // col number for (int i = 0; i < V; i++) ( if (selected(i) == true) ( for (int j = 0; j G(i)(j)) ( min = G(i)(j); x = i; y = j; ) ) ) ) ) System.out.println(x + " - " + y + " : " + G(x)(y)); selected(y) = true; no_edge++; ) ) public static void main(String() args) ( PGraph g = new PGraph(); // number of vertices in grapj int V = 5; // create a 2d array of size 5x5 // for adjacency matrix to represent graph int()() G = ( ( 0, 9, 75, 0, 0 ), ( 9, 0, 95, 19, 42 ), ( 75, 95, 0, 51, 66 ), ( 0, 19, 51, 0, 31 ), ( 0, 42, 66, 31, 0 ) ); g.Prim(G, V); ) )

 // Prim's Algorithm in C #include #include #define INF 9999999 // number of vertices in graph #define V 5 // create a 2d array of size 5x5 //for adjacency matrix to represent graph int G(V)(V) = ( (0, 9, 75, 0, 0), (9, 0, 95, 19, 42), (75, 95, 0, 51, 66), (0, 19, 51, 0, 31), (0, 42, 66, 31, 0)); int main() ( int no_edge; // number of edge // create a array to track selected vertex // selected will become true otherwise false int selected(V); // set selected false initially memset(selected, false, sizeof(selected)); // set number of edge to 0 no_edge = 0; // the number of egde in minimum spanning tree will be // always less than (V -1), where V is number of vertices in //graph // choose 0th vertex and make it true selected(0) = true; int x; // row number int y; // col number // print for edge and weight printf("Edge : Weight"); while (no_edge < V - 1) ( //For every vertex in the set S, find the all adjacent vertices // , calculate the distance from the vertex selected at step 1. // if the vertex is already in the set S, discard it otherwise //choose another vertex nearest to selected vertex at step 1. int min = INF; x = 0; y = 0; for (int i = 0; i < V; i++) ( if (selected(i)) ( for (int j = 0; j G(i)(j)) ( min = G(i)(j); x = i; y = j; ) ) ) ) ) printf("%d - %d : %d", x, y, G(x)(y)); selected(y) = true; no_edge++; ) return 0; )

 // Prim's Algorithm in C++ #include #include using namespace std; #define INF 9999999 // number of vertices in grapj #define V 5 // create a 2d array of size 5x5 //for adjacency matrix to represent graph int G(V)(V) = ( (0, 9, 75, 0, 0), (9, 0, 95, 19, 42), (75, 95, 0, 51, 66), (0, 19, 51, 0, 31), (0, 42, 66, 31, 0)); int main() ( int no_edge; // number of edge // create a array to track selected vertex // selected will become true otherwise false int selected(V); // set selected false initially memset(selected, false, sizeof(selected)); // set number of edge to 0 no_edge = 0; // the number of egde in minimum spanning tree will be // always less than (V -1), where V is number of vertices in //graph // choose 0th vertex and make it true selected(0) = true; int x; // row number int y; // col number // print for edge and weight cout << "Edge" << " : " << "Weight"; cout << endl; while (no_edge < V - 1) ( //For every vertex in the set S, find the all adjacent vertices // , calculate the distance from the vertex selected at step 1. // if the vertex is already in the set S, discard it otherwise //choose another vertex nearest to selected vertex at step 1. int min = INF; x = 0; y = 0; for (int i = 0; i < V; i++) ( if (selected(i)) ( for (int j = 0; j G(i)(j)) ( min = G(i)(j); x = i; y = j; ) ) ) ) ) cout << x << " - " << y << " : " << G(x)(y); cout << endl; selected(y) = true; no_edge++; ) return 0; )

Prim's vs Kruskal's Algorithm

Kruskala algoritms ir vēl viens populārs minimālā aptverošā koka algoritms, kas izmanto citu loģiku, lai atrastu grafika MST. Tā vietā, lai sāktu no virsotnes, Kruskaļa algoritms sašķiro visas malas no maza svara līdz lielam un turpina pievienot zemākās malas, ignorējot tās malas, kas rada ciklu.